Et me voilà donc avec une petite idée que j'avais eu il y a peut-être une année, mais sans les connaissances pour la concrétiser. Il s'agit de lancer un satellite en orbite géostationnaire au dessus d'un point précis de Kerbin. Du coup, cela ne m'a pas semblé trop compliqué à expliquer, du coup, et m'emmerdant à 1h du mat', je me suis dit que j'allais la faire partager !
Donc, pour faire un petit point sur les acronymes, déjà :
GEO = Geosynchronous Equatorial Orbit => En clair, une orbite géosynchrone équatoriale. Si son excentricité est nulle, et qu'elle est donc parfaitement circulaire, c'est une orbite géostationnaire (ce qui nous intéresse ici)
GTO = Geosynchronous Transfer Orbit => Là, c'est l'orbite qui va nous amener sur la GEO
LEO / LKO = Low Earth / Kerbin Orbit => Pas trop compliqué, ce coup-ci, c'est par exemple l'orbite que je prends à 75km après le décollage.
Déjà, pour comprendre l'idée du transfert d'orbite, utilisons le petit schéma de notre ami Wikipédia, qui ne résume pas trop mal les choses.

Comme vous pouvez le constater, on aura donc deux poussées à effectuer, représentées par des vecteurs dont la norme est DeltaV et DeltaV'.
L'orbite verte est donc notre LKO qu'on aura pris après le décollage. La jaune sera la GTO. Et la rouge sera notre objectif, c'est à dire la GEO.
Une fois ces petits préceptes théoriques acquis, il vous vient certainement une question : grâce aux manœuvres, il est relativement facile de s'orienter pour aller jusqu'à la GEO sans faire de calculs. Mais comment trouver l'endroit au dessus duquel on sera stationnaire ?
Hé bien là, pour le coup, il va falloir faire quelques calculs. Pour commencer, nous aurons besoin de la 3ème loi de Kepler, autrement appelée loi des périodes :

Où :
a = le demi grand axe de l'ellipse, en m (en gros, vous prenez la longueur de l'axe entre l'apogée et le périgée, celui qui passe par les deux foyers de l'ellipse, et vous la divisez par 2)
T = la période orbitale, en secondes (celle qui va nous intéresser)
G = la constante gravitationnelle, 6.67 x 10^-11 (l'unité... hum... non.)
M = la masse du corps de référence, en kg, ici celle de Kerbin
4 = 4 (si si)
Pi = Pi (si, je vous jure !)
A partir de là, en tournant un peu l'équation, on en déduit que :
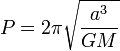
*petite coquille, ici, P = T*
Heureusement pour nous, KSP est gentil, et nous donne déjà GM, suffit d'aller sur la map et de regarder les caractéristiques de la planète (GM est aussi appelé la constante de Gauss, et se note mu, pour les curieux).
Donc GM = 3.532 x 10^12
Quant à a, il ne faut surtout pas oublier le rayon de la planète (600km).
Ainsi, considérons que l'orbite 1 est circulaire à une altitude de 75km. L'altitude de la GEO est d'environ 2869km. On a :
a = (2*600+75+2869)/2
a = 2072km
A partir de là, on est en mesure de calculer T (attention aux unités, comme diraient les profs de physique) :
T = 2 * Pi * sqrt((a^3)/GM))
T = 2 * Pi * sqrt(((2072*10^3)^3)/(3.532*10^12))
T = 9971s
Divisons par 7200 (pour trouver la moitié de cette période, et le résultat en heures), et on a 1.38h, soit 1h23.
Sachant que la période de rotation de Kerbin sur elle même est de 6h, il est possible de calculer nos coordonnées par rapport au sol avec une simple règle de trois (j'ai rien trouvé de plus élégant, mais il me semble que ça marche).
Bon, supposons que l'on veuille se mettre en orbite géostationnaire au dessus du KSC. Sa longitude est de 74.5°W (KSP nous donne les infos en degrés E, donc ça fait environ 285.5°E.
Sachant que d'un côté, on parcourt 180° en 1h23, et de l'autre, en 3h, on a qu'a calculer la distance angulaire correspondant à la rotation de Kerbin sur elle même, soit : (180/3)*1.38 = environ 83°.
Ensuite, on prend le point diamétralement opposé en longitude à celui du KSC, soit -254.5°, ou bien dans le sens "direct", 105.5°E. Et on ajoute (dans le cas d'une orbite ouest - est) les 83° à ces coordonnées, ce qui devrait nous donner de nouvelles coordonnées pour notre première poussée, et qui compensent la rotation de Kerbin. Ainsi, on a 188.5°E, soit 171.5°W. C'est donc le point au dessus duquel on va effectuer notre première poussée.
Manque de bol, KSP ne nous donne pas d'indication quant à la longitude en orbite. La solution que j'ai trouvée consiste à planter un drapeau à cet endroit là, à le targeter, et à créer un node juste en passant la distance la plus courte.
La suite, vous la connaissez certainement, il s'agit d'ajouter un node à l'apogée, puis de faire un burn de circularisation, et voilà, vous êtes en GEO !
[/s]Bon, j'ai quelques doutes quant aux calculs sur la longitude, je vais vérifier ça en jeu et voir si je me retrouve au bon endroit... Et je vous confirme (ou infirme) ça ![/s]
Bonne journée ! (oui, j'ai pas eu la foi de le finir à 1h30 en fait...)
EDIT : Ok, pas de problème du point de vue du calcul d'angle, je suis en GEO au dessus du KSC

